Study Population & Sampling

Table of Contents

Study Population & Sampling

Study population and sampling are helpful to the researcher in that it helps to classify the population that you expect to study. You are supposed to create a state that take population and provide a brief justification for this population and why you think it is the best population for this study

DEFNITIONS:

A sample: Is a subset (a part) of a population. Ideally, a researcher should use the whole population to collect data but resources may not be enough. Hence one has to resort to using a sample.

A study sample: Is a subset of the accessible population that participates in the study.

Sampling: is an act of selecting a small number of subjects upon which a study is conducted to represent the population. The result of the sample is assumed to represent the whole population. Sampling is not necessary if the population is small.

In normal circumstances, the bigger the sample size, the higher the level of accuracy.

Sample size: these are the number of respondents to get involved in the study, For example, a sample size of 150 people.

Population: Is the total of items or subjects in a set; with relevant characteristics that a researcher needs. It is the total number of potential respondents for the study.

Target population: The large set of the population to which the results will be generalized – all teenagers with asthma, for example.

Accessible population: Is the subset of the target population that is available for study – teenagers with asthma living in the investigator’s town this year, for example.

Homogeneous population: consists of subjects with specific characteristics in common.

Heterogeneous population: consists of subjects differentiated by specific identifiable features, for example, age, sex, educational background.

Sample study considers a subset of the population while census study considers/examines all members of a population.

Why (Importance of) sampling?

To manage effectively large and dispersed populations.
To minimize the cost of conducting the study.
To save time.
To improve on the accuracy of findings.
To carry out a less demanding study.
To reduce the level of destruction in case where sampling involves destroying items sampled.
Common in medical research.

Methods of sampling/Sampling Methods.

Sampling methods: A sampling method is a procedure for selecting sample elements from a population.

Random or Probability Sampling Methods
Non-random or Non-probability sampling methods.

The choice of a sampling method depends on a number of factors. Some factors are the following:

The type of population one is to sample from.
The degree of accuracy one wants.
The resources available, especially time and money.
The homogeneity of the population.
The urgency of the findings.

Random sampling method

Every element in the population has the same probability (equal chances) of selection.

Advantages of Random methods:

Offers equal chances to all members in the set to be selected.
Eliminates bias.
Improves the validity of the study.
Easy to administer.
Provides statistical means of manipulating data.

Disadvantages of Random methods:

They require a sample frame of all members of a finite population (a list of members).
There may be a possibility of un-proportional representation of strata in heterogeneous populations (over-representing or under-representing).

Random sampling methods include:

Simple random sampling.
Stratified random sampling.
Systematic sampling.
Multistage sampling.
Territorial sampling.
Cluster sampling.

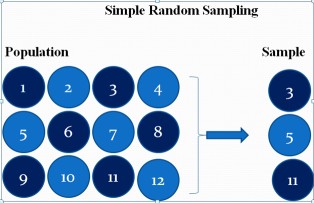
Simple random sampling:

The principle of simple random sampling is that every object has the same probability of being chosen (purely random).

There are many ways to obtain a simple random sample. One way would be the use of a lottery method.

Procedure of the lottery:

Each member of the population is assigned a unique number or name. The numbers are written on similar pieces of paper, which are folded, placed in a bowl, and thoroughly mixed.
Then, a blindfolded researcher selects one at a time without replacement until he/she has the required number of subjects in the sample.

Summary of Simple random sampling technique:

Determine the population of interest by specific characteristics.
Decide on the sample size.
Create a sample frame (list all subjects).
Select subjects randomly from the sample frame (using the lottery or a random number table).

Advantages of simple random sampling: See those for random sampling above.

Disadvantages of simple random sampling: In case of a heterogeneous population, one subgroup may be under or over-represented leading to bias.

Stratified random sampling:

A population may have subgroups in which a researcher is interested. For example, one may want to ensure that both girls and boys are represented in the sample.

The population is thus divided into subgroups or layers (strata) to represent the subgroups before the sample is drawn.

What is important is that the percentage of the subgroups in the sample must be the same as that in the population. For example, if the percentage of boys and girls in the population are 70% and 30% respectively, then the sample must also have 60% boys and 30% girls.

NB. This method uses stratifying techniques to overcome the weakness of simple random.

Stratified random sampling technique:

Decide on a sample size,
Create strata based on sound criteria (e.g., tribe),
Decide on the number of representatives to pick from each stratum, and
Randomly carry out the sampling.

Example: Consider a school with a total of 1000 students, where 600 are boys and 400 are girls, and suppose that a researcher wants to select 100 of them for a research study.

The population has 600/1000 x 100 = 60% boys.
The population has 400/1000 x 100 = 40% girls.

The sample of 100 must, therefore, have 60% boys = 60/100 x 100 = 60 boys.

Similarly, the subgroup of girls will have 40% girls in the sample = 40 girls.

Randomly carry out 60 boys from the strata of boys and 40 girls from the girls’ strata to make a sample size of 100 needed by the researcher.

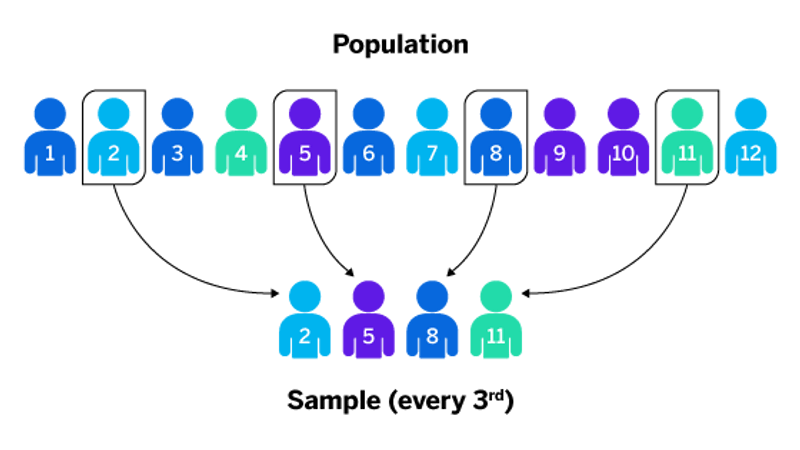
Systematic sampling:

This method relies on arranging the target population according to some ordering scheme and then selecting elements at regular intervals through that ordered list. However, to avoid bias, the starting element has to be randomly chosen.

The number in the population is divided by the required sample to get the interval.

Example: Suppose you want to sample 8 houses (sample size) from a street of 120 houses (population).

120/8 = 15 (interval), so every 15th house is chosen after a random starting point between 1 and 15. If the random starting point is 11, then the houses selected are; 11, 26, 41, 56, 71, 86, 101, and 116.

NB. This method is not purely random because some elements have more chances of being chosen than others. For example, in the above example, houses 1-15 have more chances of being selected than houses 16-120.

Systematic sampling is the best method for a big homogeneous population. It is easy to administer.

Summary of Systematic sampling process:

Define the population.
List the sample frame of all members in a certain order.
Determine the interval (population/sample size).
Systematically sample the population using the interval beginning with a random starting element.

Cluster sampling:

Cluster sampling is a type of sampling that involves dividing the population into groups (clusters). Then, one or more clusters are chosen at random (from all clusters, a random sample is made) and everyone within the chosen cluster is sampled.

The clusters are the ones that are randomly chosen.
All subjects in the random clusters are used for the study.

This method is useful when it is impossible to make a list of subjects scattered over a large area. Instead of making a list, a map of the area showing political, geographical, or other types of sub-division can be used in what we call cluster or area sampling.

Multi-stage sampling or multi-stage cluster sampling:

Using all the sample elements in all the selected clusters, as seen in cluster sampling above, may be prohibitively expensive or unnecessary. Under these circumstances, multi-stage cluster sampling becomes useful.

Instead of using all the selected clusters, the researcher randomly selects elements from each cluster; however, several levels of cluster selection are applied before the final sample elements are reached.

For example, household surveys begin by dividing metropolitan regions into ‘districts’ (first stage). The selected districts into blocks, and the blocks are chosen from each selected district (second stage).

Next, dwellings are listed within each selected block, and some of these dwellings are selected (third stage). This method makes it unnecessary to create a list of every dwelling in the region and necessary for only selected blocks.

Non-Random Sampling Methods:

These are sampling methods where some elements of the population have no chance of selection; or where the probability of selection can’t be accurately determined. They are mainly used in qualitative studies.

Advantages of Non-random sampling methods:

They are cheap.
They have a less complicated approach to sampling.
They offer faster results.
They usually do not need to have a list of all members of the population.

Disadvantages of Non-random sampling:

These methods are not random, thus prone to human error and bias.
They are better applied when research findings are not generalized beyond the sample.
Statistical analysis of sample results is not appropriate when non-random sampling methods are used. For example, a researcher cannot use statistical methods to define a confidence interval around the sample mean.

Types of non-sampling methods:

Convenient Sampling:

Sampling depends on the convenience of the researcher. The sample is selected on the basis of how accessible, convenient, and cooperative a subject may be. For example, if there are ten parishes, one can choose two parishes that are nearest to one.

Purposive/Judgmental Sampling:

The sampling depends entirely on the researcher’s interest and judgment. For example, one can choose to select only nurses on duty.

Snowball Sampling Method:

The respondents to be included in the study are recommended by colleagues who know they can offer good data. Each person interviewed suggests the next respondent to interview.

Quota Sampling:

Is a non-probability version of stratified sampling. In quota sampling, a population is first segmented into mutually exclusive sub-groups, just as in stratified sampling. Then judgment is used to select the subjects from each segment based on a specified proportion.

Accidental Sampling:

The respondents included in the study are not deliberately selected, but the sample is incidental to prevailing circumstances. For example, if you stand in front of the university gate and interview every student who passes by.

i) Sampling errors arise from drawing wrong conclusions or generalizing issues based on findings drawn from a small sample. The errors are normally less when the sample size is big, and sampling is random.

ii) Non-probability sampling does not allow the estimation of sampling error.

Sampling Errors:

The two main errors in sampling are; random error and systemic error.

Random Error: A wrong result due to chance. This can be overcome by increasing the sample size.
Systemic Error: A wrong result due to bias.

Spread the love

Study Population & Sampling